Advertisements
Advertisements
Question
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
Sum
Solution
Given: An obtuse triangle ABC, obtuse-angled at B and AD is perpendicular to CB produced.
To Prove: AC2 = AB2 + BC2 + 2BC × BD
Proof: Since ∆ADB is a right triangle right angled at D. Therefore, by
Pythagoras theorem, we have AB2 = AD2 + DB2 ….(i)
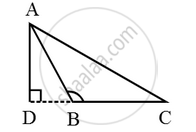
Again ∆ADC is a right triangle right angled at D.
Therefore, by Phythagoras theorem, we have
AC2 = AD2 + DC2
⇒ AC2 = AD2 + (DB + BC)2
⇒ AC2 = AD2 + DB2 + BC2 + 2BC • BD
⇒ AC2 = AB2 + BC2 + 2BC • BD [Using (i)]
Hence, AC2 = AB2 + BC2 + 2BC • BD
shaalaa.com
Is there an error in this question or solution?
