Question

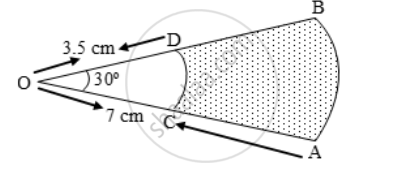
In Fig. there are shown sectors of two concentric circles of radii 7 cm and 3.5 cm. Find the area of the shaded region. Use π = `(\frac { 22 }{ 7 }).`

Answer 1

Let A₁ and A₂ be the areas of sectors OAB and OCD respectively. Then, A₁ = Area of a sector of angle 30º in a circle of radius 7 cm

`A_{1}={ \frac{30}{360}\times \frac{22}7\times 7^{2}}`

`⇒ A_1 = \frac { 77 }{ 6 } cm^2`

A₂ = Area of a sector of angle 30º in a circle of radius 3.5 cm.

∴ Area of the shaded region

`A_{2}={ \frac{30}{360}\times \frac{22}{7}\times (3.5)^{2}}`

`A_{2}={ \frac{1}{12}\times \frac{22}{7}\times\frac{7}{2}\times \frac{7}{2}}`

`=A_{1}-A_{2}=( \frac{77}{6}-\frac{77}{24})`

`= \frac { 77 }{ 24 } × (4 – 1) cm^2 = \frac { 77 }{ 8 } cm^2 = 9.625 cm^2`