Question

In the figure, given below, AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, fins the distance MN between the two chords of lengths 24 cm and 18 cm respectively.

Answer 1

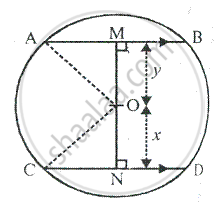
Given – AB = 24 cm, cd = 18 cm
⇒ AM = 12 cm, CN = 9 cm Also, OA = OC = 15 cm
Let MO = y cm, and ON = x cm In right angled ∆AMO
`(OA)^2 = (AM)^2 + (OM)^2`

⇒ `15^2 = 12^2 + y^2`

⇒ `y^2 = 15^2 -12^2`

⇒ `y^2 = 225 -144`

⇒` y^2 = 81`
⇒ y = 9 cm
In right angled ΔCON
`(OC)^2 = (ON)^2 + (CN)^2`

⇒ `15^2 = x^2 + 9^2`
⇒ `x^2 =15^2 - 9^2`
⇒` x^2 = 225 - 81`

⇒ `x^2 = 144`
 ⇒ y = 12 cm
Now, MN = MO + ON
= y + x
= 9 cm +12 cm
= 21 cm