Question

In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.

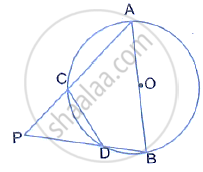
Is AC produced and BD produced meet at point P; show that ∠APB = 60°

Answer 1

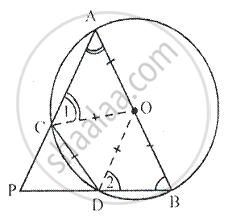
Given – In the figure, AB is the diameter of a circle with centre O. CD is the chord with length equal radius OA. AC and BD produced meet at point P To Prove : ∠APB = 60°
Construction – join OC and OD
Proof – We have CD = OC = OD [given] Therefore, ∆OCD is an equilateral triangle

∴ ∠OCD = ∠ODC = ∠COD = 60°
In ∆AOC, OA = OC [ radii of the same circle]
∴ ∠A = ∠1
Similarly, in ∆BOD, OB = OD [ radii of the same circle]
∴ ∠B = ∠2
Now, in cyclic quad ACBD Since, 

∠ACD + ∠B = 180°
[Since sum of opposite angles of a cyclic quadrilateral are supplementary]
 ⇒ 60° + ∠1+ ∠B = 180°
⇒ ∠1 + ∠B = 180° - 60°
⇒ ∠1 + ∠B = 120°
But, ∠1 = ∠A
∴ ∠A + ∠B = 120°            …..(1)

Now, in ∆APB,
∠P + ∠A + ∠B = 180° [sum of angles of a triangles]
⇒ ∠P +120° = 180°
⇒ ∠P = 180° -120°        [from (1)]
⇒ ∠P = 60° or ∠APB = 60°