Advertisements
Advertisements
Question
In the following figure, AD is a straight line. OP ⊥ AD and O is the centre of both the circles. If OA = 34 cm. OB = 20 cm and OP = 16cm; find the length of AB.
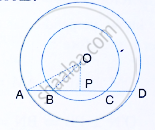
Sum
Solution
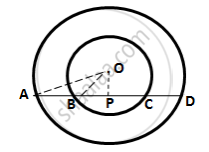
For the inner circle, BC is a chord and OP⊥ BC.
We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.
∴ BP = PC
By Pythagoras theorem,
OA2 = OP2 = BP2
⇒ BP2 = (20)2 - (16)2 =144
∴ BP= 12cm
For the outer circle, AD is the chord and OP⊥AD.
We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.
∴ AP = PD
By Pythagoras Theorem,
OA2 = OP2 + AP2
⇒ AP2 = (34)2 − (16)2 = 900
⇒ AP = 30 cm
AB = AP − BP = 30 − 12 = 18 cm
shaalaa.com
Is there an error in this question or solution?
