Question

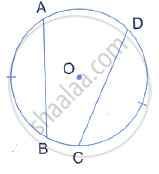
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).

Answer 1

Given –
In the figure, O is the centre of a circle and arc AB = arc CD
To prove –
ABCD is an isosceles trapezium.
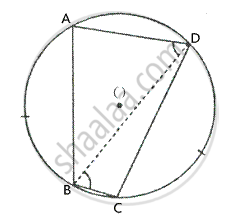
Construction – Join BD, AD and BC.
Proof – Since equal arcs subtends equal angles at the circumference of a circle.
∴ ∠ADB = ∠DBC               [∵ arc AB = arc CD]
But, these are alternate angles.
∴ AD|| BC
∴ ABCD is a trapezium
∵ Arc AB = Arc CD         [Given]
∴ Chord AB = Chord CD
∴ ABCD is an isosceles trapezium