Question

In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`

Answer 1

We know that the lengths of tangents from an exterior point to a circle are equal.

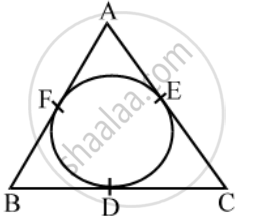
∴ AF = AE …. (i) [tangents from A]

BD = BF ….. (ii) [tangents from B]

CE =CD …. (iii) [tangents from C]

Adding (i), (ii) and (iii), we get

(AF + BD + CE) = (AE + BF + CD) = k (say)

Perimeter of ∆ABC = (AF + BD +CE) + (AE + BF + CD)

= (k + k) = 2k

`∴ k = \frac { 1 }{ 2 } "(perimeter of ∆ABC)"`

Hence AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`