Question

In the given figure, O is the centre of the circle with radius 5 cm. OP and OQ are perpendicular to AB and CD respectively. AB = 8 cm and CD = 6 cm. determine the length of PQ.

Answer 1

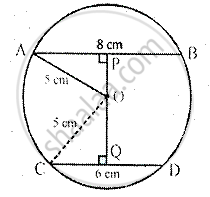
Radius of the circle whose centre is 0 = 5 cm
OP ⊥ AB and OQ ⊥ CD, AB = 8 cm and CD = 6 cm.
Join OA and OC, then OA = OC + 5 cm
Since OP ⊥ AB, P is the midpoint of AB
Similarly, Q is the midpoint of CD
In right ∆OAP,

`OA^2 = OP^2 + AP^2`    [Pythagoras Theorem]

⇒ `(5)^2 = OP^2 + (4)^2      [ ∵ AP = PB = 1/2xx 8 = 4 cm]`
⇒ ` 25 = OP^2+16`

⇒ `OP^2 = 25 -16`

⇒ `OP^2 = 9`
⇒OP = 3 cm

Similarly, in right ∆OCQ,

`OC^2 = OQ^2 + CQ^2`     [Pythagoras theorem]
⇒`(5)^2 = OQ^2 + (3)^2`

⇒`25 = OQ^2 + 9`

⇒` OQ^2 = 25 - 9`

⇒`OQ^2 = 16`
⇒ OQ = 4cm

Hence, PQ = OP + OQ = 3 + 4 = 7 cm