Advertisements
Advertisements
Question
In a hydrogen atom, the electron and proton are bound at a distance of about 0.53 Å:
(a) Estimate the potential energy of the system in eV, taking the zero of the potential energy at infinite separation of the electron from proton.
(b) What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?
(c) What are the answers to (a) and (b) above if the zero of potential energy is taken at 1.06 Å separation?
Solution
The distance between electron-proton of a hydrogen atom, d = 0.53 Å
Charge on an electron, q1 = −1.6 × 10−19 C
Charge on a proton, q2 = +1.6 × 10−19 C
(a) Potential at infinity is zero.
Potential energy of the system, = Potential energy at infinity − Potential energy at distance d
= `0 - ("q"_1"q"_2)/(4piin_0"d")`
where,
∈0 is the permittivity of free space
`1/(4piin_0) = 9 xx 10^9 "Nm"^2 "C"^-2`
∴ Potetial energy = `0 - (9 xx 10^9 xx (1.6 xx 10^-19)^2)/(0.53 xx 10^10)`
= `-43.47 xx 10^-19 "J"`
Since `1.6 xx 10^-19 "J" = 1 "eV"`
∴ Potetial energy = `-43.7 xx 10^-19 =(-43.7 xx 10^-19)/(1.6 xx 10^-19) = -27.2 "eV"`
Therefore, the potential energy of the system is −27.2 eV.
(b) Kinetic energy is half of the magnitude of potential energy.
Kinetic energy = `1/2 xx (-27.2)` = 13.6 eV
Total energy = 13.6 − 27.2 = 13.6 eV
Therefore, the minimum work required to free the electron is 13.6 eV.
(c) When zero of potential energy is taken, `"d"_1` = 1.06 Å
∴ Potential energy of the system = Potential energy at d1 − Potential energy at d
= `("q"_1"q"_2)/(4piin_0"d"_1)-27.2 "eV"`
= `(9 xx 10^9 xx (1.6 xx 10^-19)^2)/(1.06 xx 10^-10)-27.2 "eV"`
= `21.73 xx 10^-19 "J" - 27.2 "eV"`
= 13.58 eV − 27.2 eV
= −13.6 eV
APPEARS IN
RELATED QUESTIONS
A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?
We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?
Guess a possible reason why water has a much greater dielectric constant (= 80) than say, mica (= 6).
Obtain an expression for an intensity of electric field at a point at the end of position, i.e., the axial position of an electric dipole.
x
Two point charges of 10C each are kept at a distance of 3m in the vacuum. Calculate their electrostatic potential energy.
The electrostatic potential energy of two-point charges, 1 µC each, placed 1 meter apart in the air is:
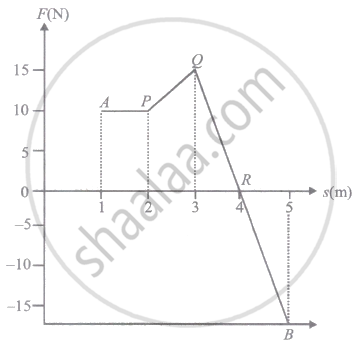
A body moves from point A to B under the action of a force, varying in magnitude as shown in the figure. Force is expressed in newton and displacement in meter. What is the total work done?
Three point charges +2, +2, and +5µC are placed respectively at the vertices A, B, C of an equilateral triangle of side 0.2 m. The magnitude of the force experienced by the charge at C is ______.
If stretch in a spring of force constant k is tripled then the ratio of elastic potential energy in the two cases will be:
Potential energy of two equal negative point charges 2µc each held lm apart in air is:-
In bringing one electron towards another electrons, the electrostatic potential energy of the system will.
When one electron is taken towards the other electron, then the electric potential energy of the system ______
A point charge q0 is moving along a circular path of radius a, with a point charge Q at the centre of the circle. The kinetic energy of q0 is ______.
