Question

In an isosceles ∆ABC, the base AB is produced both ways in P and Q such that AP × BQ = AC² and CE are the altitudes. Prove that ∆ACP ~ ∆BCQ.

Answer 1

CA = CB ⇒ ∠CAB = ∠CBA

⇒ 180º – ∠CAB = 180º – ∠CBA

⇒ ∠CAP = ∠CBQ

Now, AP × BQ = AC²

`\Rightarrow \frac{AP}{AC}=\frac{AC}{BQ}\Rightarrow\frac{AP}{AC}=\frac{BC}{BQ}`

[∵ AC = BC]

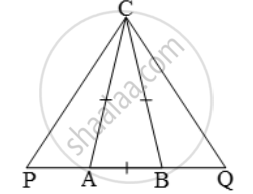
Thus, ∠CAP = ∠CBQ and ` \frac{AP}{AC}=\frac{BC}{BQ}`

∴ ∆ACP ~ ∆BCQ.