Question

In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?  

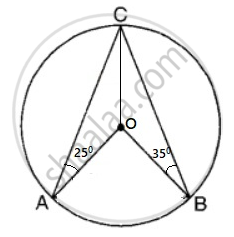
Options

• 120°

• 110°

• 55°

• Data insufficient

Answer 1

120°

Explanation:

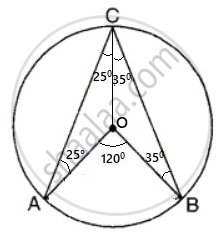
In ΔAOC,

OA = OC ................. (radii of the same circle)

∴ ΔAOC is an isosceles triangle.

→ ∠OAC = ∠OCA = 25° .................(base angles of an isosceles triangle )

In ΔBOC,

OB = OC ................. (radii of the same circle)

∴ ΔBOC is an isosceles triangle

→ ∠OBC = ∠OCB = 35° .............. (base angles of an isosceles triangle )

∠ACB = 25° + 35°= 60°

∠AOB = 2 × ∠ACB .............. (the angle at the center is twice the angle at the circumference)

= 2 × 60°

= 120°