Question

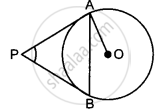
In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is ______ 

 

Options

• 30°

• 60°

• 90°

• 15°

Answer 1

In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is 30°.

Explanation:

Given ∠APB = 60°
∵ ∠APB + ∠PAB + ∠PBA = 180°
⇒ APB + x + x = 180°
[∵ PA = PB ∴ ∠PAB = ∠PBA = x (say)]
⇒ 60° + 2x = 180°
⇒ 2x = 180° - 60°
⇒ 2x = 120°
⇒ x = `(120°)/2` = 60°
Also, ∠OAP = 90°
⇒ ∠OAB + ∠PAB = 90°
⇒ ∠OAB + 60°= 90°
⇒ ∠OAB = 30°