Question

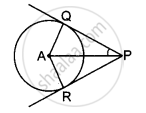
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______ 

 

Options

• 63°

• 117°

• 126°

• 153°

Answer 1

In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals 126°.

Explanation:

Here PQ and PR are tangents and AQ and AR are radii so 
∠AQP = ∠ARP = 90
Now, we know that 
AP bisects angle QPR.
 So, ∠QPR = 2∠QPA = 2 × 27 = 54 
In quadrilateral QARP, 
90 + 90 + 54 + ∠QAR = 360 
∠QAR = 126°