Question

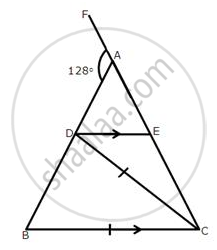
In the following figure, AB = AC; BC = CD and DE are parallel to BC.

Calculate:

1. ∠CDE
2. ∠DCE

Answer 1

∠FAB = 128°              ...[Given]

∠BAC + ∠FAB = 180°        ...[FAC is a st. line] 

⇒ ∠BAC = 180° − 128° 

⇒ ∠BAC = 52° 

In ΔABC,

∠A = 52°

∠B =  ∠C                ...[Given AB = AC and angels opposite to equal sides are equal]

∠A + ∠B + ∠C = 180°

⇒ ∠A + ∠B + ∠B = 180° 

⇒ 52° + 2∠B = 180°

⇒ 2∠B = 128°

⇒ ∠B = 64° = ∠C           ...(i)

⇒ ∠B = ∠ADE               ...[Given DE || BC]

(i) 

Now,

∠ADE + ∠CDE + ∠B = 180°       ....[ADB is a st. line]

⇒ 64° + ∠CDE + 64° = 180°

⇒ ∠CDE = 180° − 128° 

⇒ ∠CDE = 52° 

(ii)

Given DE || BC and DC is the transversal.

⇒ ∠CDE = ∠DCB = 52°             ...(ii)

Also, ∠ECB = 64°         ...[From (i)]

But,

∠ECB = ∠DCE + ∠DCB

⇒ 64° = ∠DCE + 52°

⇒ ∠DCE = 64° − 52°

⇒ ∠DCE = 12°