Advertisements
Advertisements
Question
In the give figure, if DPQR is an isosceles triangle, prove that: ∠QSR = exterior ∠PRT.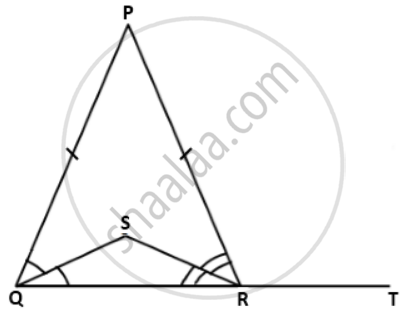
Sum
Solution

Let ∠PQS = ∠SQR = x and ∠PRS = ∠SRQ = y
In ΔPQR,
∠QPR + ∠PQR + ∠PRQ = 180°
⇒ ∠QPR + 2x + 2y = 180°
⇒ ∠QPR = 180° - 2x - 2y ....(i)
Since PQ = PR,
∠PRQ = ∠PQR ....(angles opposite to two equal sides are equal)
⇒ 2x = 2y
⇒ x = y
Now, ∠PRT = ∠PQR + ∠QPR ....(by exterior angle property)
⇒ ∠PRT = 2x + 180° - 2x - 2y ....(From (i)]
⇒ ∠PRT = 180° - 2y ....(ii)
In ΔSQR,
∠QSR + ∠SQR + ∠SRQ = 180°
⇒ ∠QSR + x + y = 180°
⇒ ∠QSR = 180° - x - y
⇒ ∠QSR = 180° - y - y ....[∵ x = y (proved)]
⇒ ∠QSR = 180° - 2y ....(iii)
From (ii) and (iii),
∠QSR = ∠PRT.
shaalaa.com
Is there an error in this question or solution?
