Question

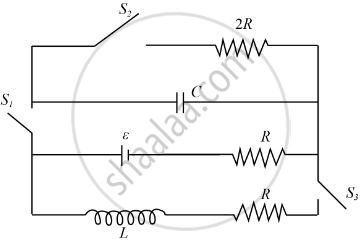
In the given circuit, initially switch S₁ is closed and S₂ and S₃ are open. After charging of capacitor, at t = 0, S₁ is open and S₂ and S₃ are closed. If the relation between inductance capacitance and resistance is L = 4CR² then the time (in sec) after which current passing through capacitor and inductor will be same is ______ × 10^-4 N. (Given R = ℓn(2)_mΩ, L = 2mH)

Options

• 1

• 2

• 3

• 4

Answer 1

In the given circuit, initially switch S₁ is closed and S₂ and S₃ are open. After charging of capacitor, at t = 0, S₁ is open and S₂ and S₃ are closed. If the relation between inductance capacitance and resistance is L = 4CR² then the time (in sec) after which current passing through capacitor and inductor will be same is 1 × 10^-4 N. (GivenR = ℓn(2)_mΩ, L = 2mH)

Explanation:

After charging, charge on capacitor = Cε

Now at t = 0 two circuits formed

1. Discharging of capacitor

∴ q = C ε e^-t/τ_L

= C ε `"e"^(-"t"//2"RC")`

∴ i₁ = `epsilon/(2"R")"e"^(-"t"//2"RC")` 

2. Growth of current in L-R circuit

i₂ = `epsilon/(2"R")` [1 - e^-t/τ_L]

now i₁ = i₂

`epsilon/(2"R") e^(-t//τ_"L") = epsilon/(2"R") [1-e^(-t//τ_"L")]`

given L = 4CR²

∴ `"L"/(2"R") = 2"RC" = 1/("In"  2)`

⇒ ln from equation (1) 2 `e^(-"t"  "In"2)` = 1

⇒ t ln2 = ln2

⇒ t = 1 sec