Question

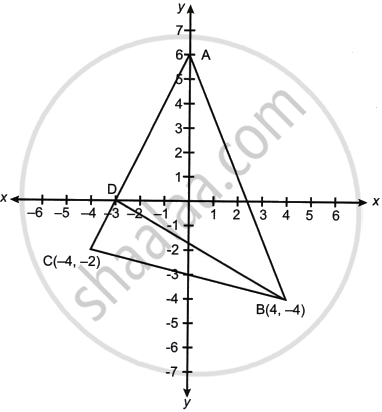
In the given diagram, ABC is a triangle, where B(4, – 4) and C(– 4, –2). D is a point on AC.

1. Write down the coordinates of A and D.
2. Find the coordinates of the centroid of ΔABC.
3. If D divides AC in the ratio k : 1, find the value of k.
4. Find the equation of the line BD.

Answer 1

a. Coordinates of A = (0, 6)

Coordinates of D = (–3, 0)

b. Here, coordinates of A = (0, 6)

Coordinates of B = (4, –4)

Coordinates of C = (–4, –2)

Then, coordinates of centroid are

`((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`

= `((0 + 4 + (-4))/3, (6 + (-4) + (-2))/3)`

= `(0/3, 0/3)`

= (0, 0)

c. Here, x₁ = – 4, y₁ = – 2

x₂ = 0, y₂ = 6

m₁ = k, m₂ = 1

x = – 3, y = 0

By section formula,

D(x, y) = `((m_1x_2 + m_2x_1)/(m_1 + m_2), (m_1y_2 + m_2y_1)/(m_1 + m_2))` 

D(– 3, 0) = `((k xx 0 + 1 xx (-4))/(k + 1), (k xx 6 + 1 xx (-2))/(k + 1))`

∴ – 3 = `(-4)/(k + 1)` or 0 = `(6k - 2)/(-k + 1)`

`\implies` –3k – 3 = – 4 or 6k – 2 = 0

`\implies` – 3k = – 1 or 6k = 2

k = `1/3` or k = `1/3`

Hence, k = `1/3`

d. Coordinates of B = (4, – 4)

Coordinates of D = (–3, 0)

Then, equation of line BD is:

`(y - y_1) = (y_2 - y_1)/((x_2 - x_1)) (x - x_1)`

`\implies [y - (-4)] = ([0 - (-4)])/((-3 - 4)) (x - 4)`

`\implies (y + 4) = 4/(-7) (x - 4)`

`\implies` –7(y + 4) = 4(x – 4)

`\implies` –7y – 28 = 4x – 16

`\implies` 4x – 16 + 7y + 28 = 0

`\implies` 4x + y + 12 = 0, is the required equation