Question

In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:

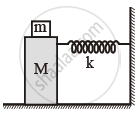
Options

• `"A"sqrt("M"/("M"+"m"))`

• `"A"sqrt("M"/("M"-"m"))`

• `"A"sqrt(("M"-"m")/"M")`

• `"A"sqrt(("M"+"m")/"M")`

Answer 1

`bb("A"sqrt("M"/("M"+"m")))`

Explanation:

As there are no impulsive forces, momentum will always be conserved.

`"MA"((2pi)/"T"_1) = ("m"+"M") "A"_1 ((2pi)/"T"_2)`    ...(i)

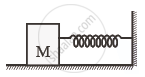
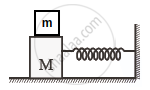
T₁ = 2π `sqrt("M"/"K")`

T2 = 2π `sqrt(("M"+"m")/"K")`

Now, substituting the value of T₁ and T₂ in equation (i).

`"MA"((2pi)/(2pisqrt("M"/"K"))) = ("m"+"M" )  "A"_1 ((2pi)/(2pisqrt(("M"+  "m")/"K")))`

⇒ A₁ = `("MA"sqrt"K"/"M")/(("m"+"M")sqrt("K"/("M"+  "m")))`

⇒ A₁ = A `sqrt"M"/("M"+"m")`