Question

In the given figure, ABCD is a quadrilateral. Diagonal BD bisects ∠B and ∠D both.

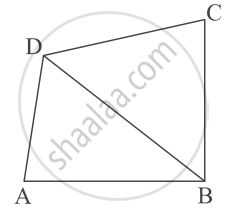
Prove that: 

1. ΔABD ~ ΔCBD 
2. AB = BC

Answer 1

i. Given: diagonal BD bisects ∠B and ∠D

To prove: ΔABD ∼ ΔCBD

Proof: In ΔABD and ΔCBD

∠ABD = ∠CBD      ...(BD bisects ∠B)

∠ADB = ∠CDB     ....(BD bisects ∠D)

Therefore, ΔABD ∼ ΔCBD     ...(by AA rule)

Hence proved

ii. Since, ΔABD ∼ ΔCBD

Therefore, `(AB)/(BD) = (BC)/(BD)`     ...(by cpct)

∴ AB = BC   Hence Proved.