Advertisements
Advertisements
Question
In the given figure, area of ∆AFB is equal to the area of parallelogram ABCD. If altitude EF is 16 cm long, find the altitude of the parallelogram to the base AB of length 10 cm. What is the area of ∆DAO, where O is the midpoint of DC?
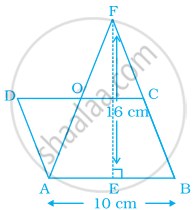
Solution
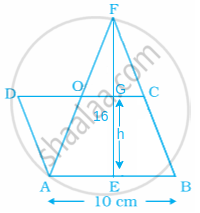
Given, Area of ΔAFB = Area of parallelogram ABCD
⇒ `1/2` × AB × EF = CD × (Corresponding height) ......`[(∵ "area of triangle" = "base" xx "height and area of"),("parallelogram" = "base" xx "corresponding height")]`
⇒ `1/2` × AB × EF = CD × EG
Let the corresponding height be h.
Then, `1/2` × 10 × 6 = 10 × h ......[∵ altitude, EF = 16 cm and base, AB = 10 cm, given] [∵ AB = CD]
⇒ h = 8 cm
In ΔDAO, DO = 5 cm .....[∵ O is the mid-point of CD]
∴ Area of ΔDAO = `1/2` × OD × h
= `1/2 xx 5 xx 8`
= 20 cm2
APPEARS IN
RELATED QUESTIONS
Find the area of the following parallelogram:
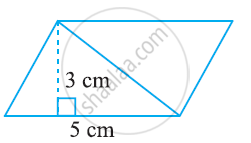
Find the area of the following parallelogram:

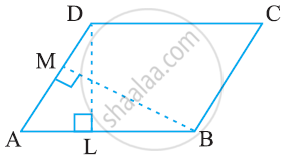
DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (see the given figure). If the area of the parallelogram is 1470 cm2, AB = 35 cm and AD = 49 cm, find the length of BM and DL.
Find the missing values.
| Base | Height | Area |
| 8 cm | 56 sq.m |
The area of parallelogram whose base 10 m and height 7 m is
The base of the parallelogram with area is 52 sq.cm and height 4 cm is
The base of the parallelogram is 16 cm and the height is 7 cm less than its base. Find the area of the parallelogram
The height of the parallelogram is one-fourth of its base. If the area of the parallelogram is 676 sq.cm, find the height and the base
In a parallelogram PQRS (See the diagram) PM and PN are the heights corresponding to the sides QR and RS respectively. If the area of the parallelogram is 900 sq.cm and the length of PM and PN are 20 cm and 36 cm respectively, find the length of the sides QR and SR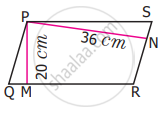
If the sides of a parallelogram are increased to twice its original lengths, how much will the perimeter of the new parallelogram?
