Advertisements
Advertisements
Question
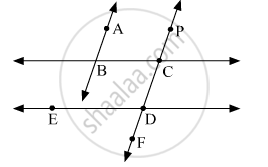
In the given figure, if line AB || line CF and line BC || line ED then prove that ∠ABC = ∠FDE.
Solution

Let us mark the points M and N on line BC and point G on line ED.
Since line AB || line PF (or line CF) and line MN is their transversal,
∠PCN = ∠ABC ...(Corresponding angles)...(1)
Since line MN || line EG and line PF is their transversal, then
∠PCN = ∠CDG ...(Corresponding angles)...(2)
Since EG and PF are straight lines intersecting at D, then
∠CDG = ∠FDE ...(Vertically opposite angles) ...(3)
∴ from (2) and (3), we get
∠PCN = ∠FDE ...(4)
∴ from (1) and (4), we get
∠ABC = ∠FDE
APPEARS IN
RELATED QUESTIONS
In the given figure, y = 108° and x = 71° Are the lines m and n parallel? Justify.

In the figure, ray AE || ray BD, ray AF is the bisector of ∠EAB and ray BC is the bisector of ∠ABD. Prove that line AF || line BC.

A transversal EF of line AB and line CD intersects the lines at point P and Q respectively. Ray PR and ray QS are parallel and bisectors ∠BPQ and ∠PQC respectively. Prove that line AB || line CD.

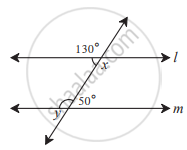
In the given figure, measures of some angles are shown. Using the measures find the measures of ∠x and ∠y and hence show that line l || line m.
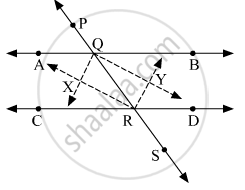
In the given figure, line PS is a transversal of parallel line AB and line CD. If Ray QX, ray QY, ray RX, ray RY are angle bisectors, then prove that `square` QXRY is a rectangle.