Advertisements
Advertisements
Question
In the given figure, points G, D, E, and F are concyclic points of a circle with centre C. ∠ECF = 70°, m(arc DGF) = 200°. Find m(arc DE) and m(arc DEF).
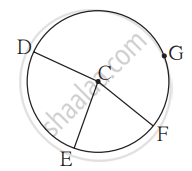
Sum
Solution
m(arc EF) = m∠ECF ...(Definition of measure of minor arc)
∴ m(arc EF) = 70º
(i) m(arc DE) + m(arc DGF) + m(arc EF) = 360º ...(Measure of a circle is 360º)
∴ m(arc DE) + 200° + 70º = 360º
∴ m(arc DE) = 360º − 200° − 70º
∴ m(arc DE) = 90º
(ii) m(arc DEF) = m(arc DE) + m(arc EF) ...(Arc addition property)
∴ m(arc DEF) = 90º + 70º
∴ m(arc DEF) = 160º
Thus, m(arc DE) = 90º and m(arc DEF) = 160º.
shaalaa.com
Is there an error in this question or solution?
