Advertisements
Advertisements
Question
In triangle ABC; ∠A = 60o, ∠C = 40o, and the bisector of angle ABC meets side AC at point P. Show that BP = CP.
Solution
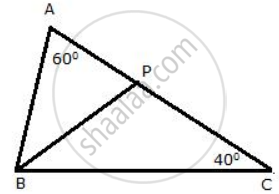
In ΔABC,
∠A = 60°
∠C = 40°
∴ ∠B = 180° - 60° - 40°
⇒ ∠B = 80°
Now,
BP is the bisector of ∠ABC.
∴ ∠PBC = ` "∠ABC"/2`
⇒ ∠PBC = 40°
In ΔPBC,
∠PBC = ∠PCB = 40°
∴ BP = CP ....[ Sides opp. to equal angles are equal.]
APPEARS IN
RELATED QUESTIONS
Find the values of x and y using the information shown in the figure.

Find the measure of ∠ABD and m∠ACD.
ΔABC is isosceles in which AB = AC. Seg BD and seg CE are medians. Show that BD = CE.
In triangle ABC, D is a point in AB such that AC = CD = DB. If ∠B = 28°, find the angle ACD.
ABC is an equilateral triangle. Its side BC is produced up to point E such that C is mid-point of BE. Calculate the measure of angles ACE and AEC.
In triangle ABC; angle ABC = 90o and P is a point on AC such that ∠PBC = ∠PCB.
Show that: PA = PB.
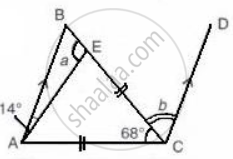
Using the information given of the following figure, find the values of a and b. [Given: CE = AC]
In triangle ABC, AB = AC; BE ⊥ AC and CF ⊥ AB.
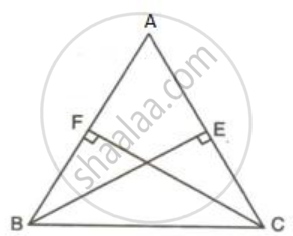
Prove that:
(i) BE = CF
(ii) AF = AE
Through any point in the bisector of an angle, a straight line is drawn parallel to either arm of the angle. Prove that the triangle so formed is isosceles.
If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
