Question

In triangle ABC, AB = AC and ∠A= 36°. If the internal bisector of ∠C meets AB at point D, prove that AD = BC.

Answer 1

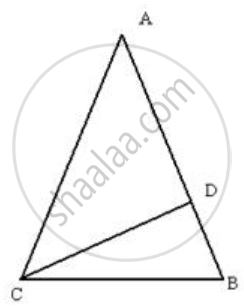
AB = AC
ΔABC is an isosceles triangle.
∠A = 36°
∠B = C = `[180° - 36°]/2` = 72°

∠ACD = ∠BCD = 36° .......[∵ CD is the angle bisector of ∠C]
ΔADC is an isoscelsss traingle since ∠DAC = ∠DCA = 36°
∴  AD = CD .......(i)

In ΔDCB,
∠CDB = 180° − ( ∠DCB +∠DBC )
        = 180° − ( 36° + 72° )
        =  180° − 108°
         = 72°

ΔDCB is an isosceles triangle since ∠CDB = ∠CBD = 72°
∴  DC = BC ......(ii)
From (i) and (ii), we get
AD = BC
Hence proved.