Question

In triangle ABC; AB = AC. P, Q, and R are mid-points of sides AB, AC, and BC respectively.
Prove that: BQ = CP

Answer 1

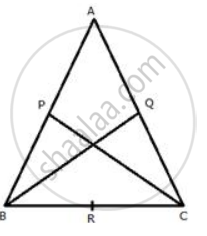
AB = AC
⇒ ∠B = ∠C
Also,
`1/2"AB" = 1/2"AC"`
⇒ BP = CQ                  ...[ P and Q are mid-points of AB and AC ]

In ΔBPC and ΔCQB,
BP = CQ
∠B = ∠C
BC = BC
Therefore, ΔBPC ≅ ΔCQB    ...[ SAS ]
BP = CP.