Question

In triangle ABC, the bisector of angle BAC meets the opposite side BC at point D. If BD = CD, prove that ΔABC is isosceles.

Answer 1

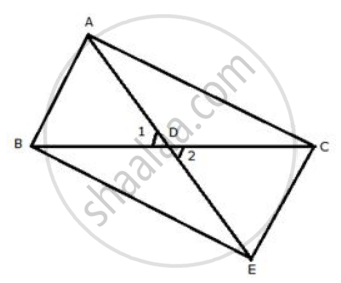
Produce AD up to E such that AD = DE.
In ΔABD and ΔEDC,
AD = DE                     ...[ by construction ]
BD = CD                     ...[ Given ]
∠1= ∠2                       ...[ Vertically opposite angles ]
∴ ΔABD ≅ ΔEDC        ...[ SAS ]
⇒ AB = CE                 ...(i)
and ∠BAD = ∠CED
but, ∠BAD = ∠CAD     ...[ AD is bisector of ∠BAC ]
∴ ∠CED = ∠CAD
⇒ AC = CE                  ...(ii)
From (i) and (ii)
AB = AC
Hence, ABC is an isosceles triangle.