Advertisements
Advertisements
Question
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
Sum
Solution
Let AB and CD be two chords of the circle which touch the inner circle at M and N respectively.
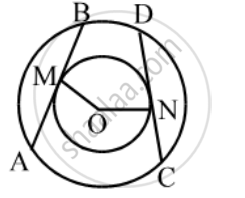
Then, we have to prove that
AB = CD
Since AB and CD are tangents to the smaller circle.
∴ OM = ON = Radius of the smaller circle
Thus, AB and CD are two chords of the larger circle such that they are equidistant from the centre. Hence, AB = CD
shaalaa.com
Is there an error in this question or solution?
