Advertisements
Advertisements
Question
Is it possible to design a rectangular park of perimeter 320 m and area 4800 m2? If so find its length and breadth.
Advertisements
Solution
Let the length of the rectangular park be “l”
and the breadth of the rectangular park be “b”
Perimeter of the park = 320 m
2 (l + b) = 320
l + b = 160
l = 160 – b ...(1)
Area of the park = 4800 m2
l × b = 4800 ...(2)
substitute the value of l = 160 – b in (2)
(160 – b)b = 4800
160b – b2 = 4800
b2 – 160b + 4800 = 0
(b – 120) (b – 40) = 0
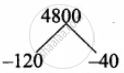
b = – 120 = 0 or b – 40 = 0
b = 120 or b = 40
If breadth is 120 length is 40
If breadth is 40 length is 120
Length of the park = 120 m
Breadth of the park = 40 m
APPEARS IN
RELATED QUESTIONS
Simplify `(x + 4)/(3x + 4y) xx (9x^2 - 16y^2)/(2x^2 + 3x - 20)`
If a polynomial p(x) = x2 – 5x – 14 is divided by another polynomial q(x) we get `(x - 7)/(x + 2)`, find q(x)
Simplify `(x(x + 1))/(x - 2) + (x(1 - x))/(x - 2)`
Simplify `((2x + 1)(x - 2))/(x - 4) - ((2x^2 - 5x + 2))/(x - 4)`
Simplify `(4x)/(x^2 - 1) - (x + 1)/(x - 1)`
Identify rational expression should be subtracted from `(x^2 + 6x + 8)/(x^3 + 8)` to get `3/(x^2 - 2x + 4)`
`(3y - 3)/y ÷ (7y - 7)/(3y^2)` is
At t minutes past 2 pm, the time needed to 3 pm is 3 minutes less than `("t"^2)/4`. Find t.
Two farmers Thilagan and Kausigan cultivates three varieties of grains namely rice, wheat and ragi. If the sale (in ₹) of three varieties of grains by both the farmers in the month of April is given by the matrix.
`{:("April sale in" ₹)/("rice" "wheat" "ragi"):}`
A = `[(500, 1000, 1500),(2500, 1500, 500)]"Thilagan"/"Kausigan"`
and the May month sale (in ₹) is exactly twice as that of the April month sale for each variety.
What is the average sales for the months of April and May
Two farmers Thilagan and Kausigan cultivates three varieties of grains namely rice, wheat and ragi. If the sale (in ₹) of three varieties of grains by both the farmers in the month of April is given by the matrix.
`{:"April sale in" ₹)/("rice" "wheat" "ragi":}`
A = `[(500, 1000, 1500),(2500, 1500, 500)]"Thilagan"/"Kausigan"`
and the May month sale (in ₹) is exactly twice as that of the April month sale for each variety.
If the sales continue to increase in the same way in the successive months, what will be sales in the month of August?
