Advertisements
Advertisements
Question
ज्या त्रिकोणाची परिमिती 14.4 सेमी आहे आणि ज्याच्या बाजूंचे गुणोत्तर 2 : 3 : 4 आहे, असा त्रिकोण काढा.
Solution 1
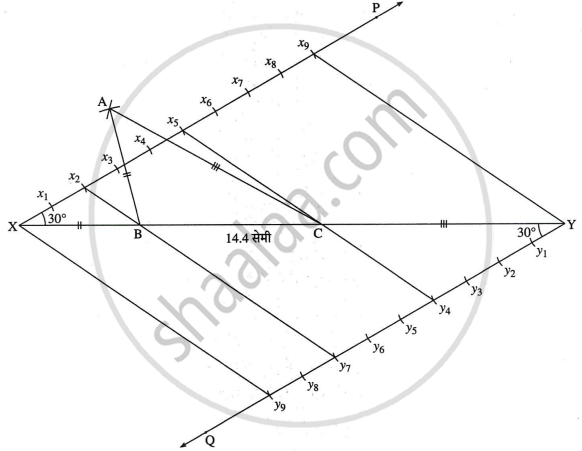
स्पष्टीकरण:
माना ΔABC हा अपेक्षित त्रिकोण आहे.
रेखा XY = 14.4 सेमी काढा, जे ΔABC ची परिमिती आहे.
आपल्याला रेखा XY ला 2:3:4 च्या अनुपातात विभाजित करायचे आहे.
किरण XP असा काढा की, ∠YXP = 30°
किरण XP च्या विपरीत बाजूला रेखा YQ असे काढा की, ∠XYQ = 30°
किरण XP चे 9 समान भाग करा, म्हणजेच `"X"_(x_1)`, x1x2, ... ,x8x9 तयार करा.
त्याच प्रकारे, आकृतीप्रमाणे, किरण YQ चे 9 समान भाग करा.
x2y7 आणि x5y4 जोडा, जे रेखा XY ला अनुक्रमे B आणि C बिंदूंत छेदतात.
B केंद्र व BX एवढी त्रिज्या घेऊन किरण XP च्या वरच्या बाजूस कंस काढा.
C केंद्र व CY एवढी त्रिज्या घेऊन किरण XP च्या वरच्या. बाजूस आधी काढलेल्या कंसाला छेदणारा दुसरा कंस काढा.
रेखा AB आणि रेखा AC काढा.
ΔABC हा अपेक्षित त्रिकोण आहे.
Solution 2
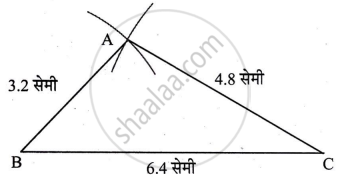
कच्ची आकृती:
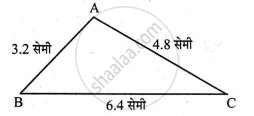
स्पष्टीकरण:
समजा, सामाईक गुणक x आहे.
∴ ∆ABC मध्ये,
AB = 2x सेमी, AC = 3x सेमी, BC = 4x सेमी
त्रिकोणाची परिमिती = 14.4 सेमी
∴ AB + BC + AC = 14.4
∴ 9x = 14.4
∴ `x = 14.4/9`
∴ x = 1.6
∴ AB = 2x = 2 × 1.6 = 3.2 सेमी
∴ AC = 3x = 3 × 1.6 = 4.8 सेमी
∴ BC = 4x = 4 × 1.6 = 6.4 सेमी