Advertisements
Advertisements
Question
किसी खोखले आवेशित चालक में उसके पृष्ठ पर कोई छिद्र बनाया गया है। यह दर्शाइए कि छिद्र में विद्युत-क्षेत्र (σ/2ε0) `hat"n"` है, जहाँ `hat"n"` अभिलम्बवत् दिशा में बहिर्मुखी एकांक सदिश है तथा σ छिद्र के निकट पृष्ठीय आवेश घनत्व है।
Solution
माना किसी खोखले चालक को कुछ धनावेश दिया गया है, जो तुरन्त ही उसके पृष्ठ पर समान रूप से वितरित हो जाता है। माना आवेश का पृष्ठ घनत्व σ है। चालक के पृष्ठ के किसी अवयव dA पर विचार कीजिए। स्पष्ट है कि इस क्षेत्रफल अवयव पर उपस्थित आवेश की मात्रा q = σ dA होगी। माना इस क्षेत्रफल अवयव के अत्यन्त समीप चालक के पृष्ठ के बाहर तथा अन्दर दो बिन्दु क्रमश: P तथा Q हैं। चूँकि बिन्दु P पृष्ठ के समीप है; अतः चालक के कारण बिन्दु P पर विद्युत-क्षेत्र की तीव्रता E = \[\ce{\frac{\sigma}{{\epsilon}_{0}}}\] पृष्ठ के लम्बवत् बाहर की ओर होगी। माना बिन्दु P पर अवयव dA तथा शेष चालक के कारण विद्युत-क्षेत्र की तीव्रताएँ क्रमश: E1 व E2 हैं, तब स्पष्टतया E1 व E2 दोनों पृष्ठ के लम्बवत् बाहर की ओर होंगी तथा परिणामी तीव्रता E, E1 व E2 के योग के बराबर होगी।
अतः E1 + E2 = \[\ce{\frac{\sigma}{{\epsilon}_{0}}}\] …..(1)
चूँकि बिन्दु Q क्षेत्रफल अवयव dA के अत्यन्त समीप परन्तु P के विपरीत ओर है; अतः इस अवयव के कारण बिन्दु Q पर क्षेत्र की तीव्रता E1 के बराबर परन्तु दिशा में विपरीत होगी, जबकि शेष चालक के कारण Q पर विद्युत-क्षेत्र की तीव्रता E2 के बराबर तथा उसी की दिशा में होगी। चूँकि बिन्दु Q चालक के अन्दर है; अतः बिन्दु Q पर परिणामी तीव्रता शून्य होगी।
अतः बिन्दु Q पर परिणामी तीव्रता E2 – E1 = 0
अथवा E1 = E2 [बिन्दु Q पर E1 व E2 के विपरीत हैं।]
समीकरण (1) से, E1 = E2 = \[\ce{\frac{\sigma}{2{\epsilon}_{0}}}\]
अतः शेष चालक के कारण बिन्दु P पर विद्युत-क्षेत्र की तीव्रता
E2 = \[\ce{\frac{\sigma}{2{\epsilon}_{0}}}\] अब यदि बिन्दु P पर एक छिद्र कर दिया जाए तो क्षेत्र अवयव dA तथा इसके कारण आन्तरिक बिन्दु Q पर विद्युत-क्षेत्र E1 दोनों समाप्त हो जाएँगे।
तब विद्युत-क्षेत्र E2 छिद्र के किसी बिन्दु पर केवल शेष चालक के कारण शेष रहेगा।
अतः छिद्र पर विद्युत-क्षेत्र की तीव्रता
\[\ce{\overset{\rightarrow}{E} = \frac{\sigma}{2{ \epsilon}_{0}}\overset{\wedge}{n}}\]
जहाँ n छिद्र पर बहिर्मुखी दिशा में एकांक सदिश है।
APPEARS IN
RELATED QUESTIONS
4 × 10-9 C m द्विध्रुव आघूर्ण को कोई विद्युत-द्विध्रुव 5 × 104 NC-1 परिमाण के किसी एकसमान विद्युत-क्षेत्र की दिशा से 30° पर संरेखित है। द्विध्रुव पर कार्यरत बल आघूर्ण का परिमाण परिकलित कीजिए।
किसी चालक A, जिसमें निचे दिए गए चित्र में दर्शाए अनुसार कोई कोटर/गुहा (Cavity) है, को Q आवेश दिया गया है। यह दर्शाइए कि समस्त आवेश चालक के बाह्य पृष्ठ पर प्रतीत होना चाहिए।
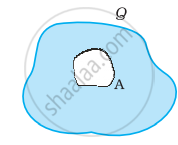
निचे दिए गए चित्र में कोई अन्य चालक B जिस पर आवेश q है, को कोटर/गुहा (Cavity) में इस प्रकार सँसा दिया जाता है कि चालक Bचालक A से विद्युतरोधी रहे। यह दर्शाइए कि चालक A के बाह्य पृष्ठ पर कुल आवेश Q + q है।
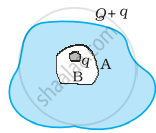
किसी सुग्राही उपकरण को उसके पर्यावरण के प्रबल स्थिर विद्युत-क्षेत्रों से परिरक्षित किया जाना है। सम्भावित उपाय लिखिए।
