Question

Let A = [a_ij] be a 3 × 3 matrix, where

a_ij = `{{:(1, "," if "i" = "j"),(-x, "," if |"i" - "j"| = 1),(2x + 1, ","    "otherwise"):}` 

Let a function f: R→R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to ______.

Options

• `20/27`

• `-88/27`

• `-20/27`

• `88/27`

Answer 1

Let A = [a_ij] be a 3 × 3 matrix, where

a_ij = `{{:(1, "," if "i" = "j"),(-x, "," if |"i" - "j"| = 1),(2x + 1, ","    "otherwise"):}` 

Let a function f: R→R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to `underlinebb(-88/27)`.

Explanation:

|A| = `|(1, -x, 2x + 1),(-x, 1, -x),(2x + 1, -x, 1)|`

= 1(1 – x²) + x(–x + x(2x + 1)) + (2x + 1)(x² –(2x + 1))

= 1 + x²(2x + 1) + x²(2x + 1) – (2x + 1)² – x² – x²

⇒ f(x) = 4x³ – 4x² – 4x

⇒ f'(x) = 12x² – 8x – 4

⇒ f'(x) = 4(3x² – 2x – 1) = 4(x – 1)(3x + 1)

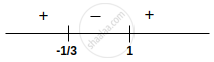sign of f'

⇒ f(x) is maximum at x = `(-1)/3` and minimum at x = 1

Maximum value = `f((-1)/3) = 20/27`

Minimum value f(1) = –4

∴ Sum = `20/27 - 4 = (-88)/27`