Question

Let a and b are two positive integers such that b ≠ 1. Let g(a, b) = Number of lattice points inside the quadrilateral formed by lines x = 0, y = 0, x = b and y = a. f(a, b) = `[a/b] + [(2a)/b] + ... + [((b - 1)a)/b]`, then the value of `[(g(101, 37))/(f(101, 37))]` is ______.

(Note P(x, y) is lattice point if x, y ∈ I)

(where [.] denotes greatest integer function)

Options

• 0.00

• 1.00

• 2.00

• 3.00

Answer 1

Let a and b are two positive integers such that b ≠ 1. Let g(a, b) = Number of lattice points inside the quadrilateral formed by lines x = 0, y = 0, x = b and y = a. f(a, b) = `[a/b] + [(2a)/b] + ... + [((b - 1)a)/b]`, then the value of `[(g(101, 37))/(f(101, 37))]` is 2.00.

(Note P(x, y) is lattice point if x, y ∈ I)

(where [.] denotes greatest integer function)

Explanation:

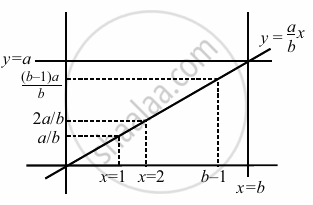
g(a, b) = (a – 1) (b – 1)

f(a, b) = `((a - 1)(b - 1))/2`

Now, `[(g(101, 37))/(f(101, 37))]`

= `((100 xx 36)/((100 xx 36)))/2`

= 2