Question

Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x³ – 3x² – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.

Options

• 112

• 113

• 114

• 115

Answer 1

Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x³ – 3x² – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to 114.

Explanation:

Given f(x) = 2x³ – 3x² – 12x

f'(x) = 6x² – 6x – 12 = 6(x – 2) (x + 1)

Point = (2, –20) and (–1, 7)

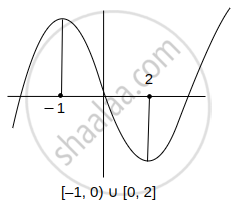
A = `int_-1^0(2x^3 - 3x^2 - 12x)dx + int_0^2(12x + 3x^2 - 2x^3)dx`

A = `(x^4/2 - x^3 - 6x^2)_-1^0 + (6x^2 + x^3 - x^4/2)_0^2`

= `-(1/2 + 1 - 6) - (8 - 8 - 24)`

A = `57/2`, 4A = `4 xx 57/2` = 114