Question

Let arg (z) represent the principal argument of the complex number z. Then, |z| = 3 and arg (z – 1) – arg (z + 1) = `π/4`intersect ______.

Options

• Exactly at one point.

• Exactly at two points.

• Nowhere

• At infinitely many points.

Answer 1

Let arg (z) represent the principal argument of the complex number z. Then, |z| = 3 and arg (z – 1) – arg (z + 1) = `π/4`intersect nowhere.

Explanation:

Given: |z| = 3

⇒ It represents a circle of radius 3 and centre at (0, 0)

And arg (z – 1) – arg (z + 1) = `π/4`

⇒ agr`((z - 1)/(z + 1)) = π/4`

⇒ z is on major are of circle having PQ as chord and R(0, a) as centre of the circle.

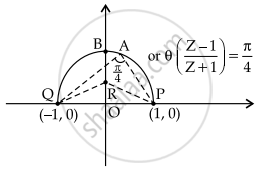
So, ∠PAQ = ∠ORP = `π/4`

⇒ OP = OR = a = 1

∴ Coordinates of R is (0,1)

So, radius = RP = `sqrt(2)`

∴ OB = OR + `sqrt(2) = 1 + sqrt(2)`

⇒ B = `(0, 1 + sqrt(2))`

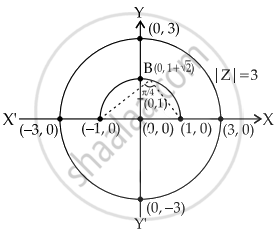
So, it is clear from the figure, both curves do not intersect.

∴ No z satisfy both equation.