Question

Let P: y² = 4ax, a > 0 be a parabola with focus S. Let the tangents to the parabola P make an angle of `π/4` with the line y = 3x + 5 touch the parabola P at A and B. Then the value of a for which A, B and S are collinear is ______.

Options

• 8 Only

• 2 Only

• `1/4` Only

• Any a > 0

Answer 1

Let P: y² = 4ax, a > 0 be a parabola with focus S. Let the tangents to the parabola P make an angle of `π/4` with the line y = 3x + 5 touch the parabola P at A and B. Then the value of a for which A, B and S are collinear is any a > 0.

Explanation:

P: y² = 40x, a > 0

And tangents to the parabola makes an angle of `π/4` with y = 3x + 5

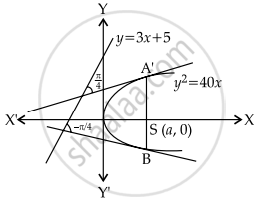
Let slope of tangent be m.

∴ `tan  π/4 = |(m - 3)/(1 + 3m)|`

⇒ 1 = `|(m - 3)/(1 + 3m)|`

⇒ `|(m - 3)/(1 + 3m)|` = ±1

⇒ `(m - 3)/(1 + 3m)` = 1 and `(m - 3)/(1 + 3m)` = –1

⇒ m = –2 and m = `1/2`

∴ Point of contact are `B(a/(-2)^2, (2a)/(-2))` and `A(a/(1/2)^2, (2a)/(1/2))`

⇒ `B(a/4, -a)` and A(4a, 4a)

∵ Points A, S and B are collinear.

⇒ `|(4a, 4a, 1),(a/4, -a, 1),(a, 0, 1)|` = 0

⇒ `4a(-a) - 4a(a/4 - a) + 1(a^2)` = 0

⇒ –4a² + 3a² + a² = 0

⇒ 0 = 0

∴  Points A, S and B are always collinear for A ∈ R.