Question

Let the straight line x = b divide the area enclosed by y = (1 - x)², y = 0 and x = 0 into two parts R₁(0 ≤ x ≤ b) and R₂ (b ≤ x ≤ 1) such that `R_1 - R_2 = 1/4`. Then b equals ______ 

Options

• `3/4`

• `1/2`

• `1/3`

• `1/4`

Answer 1

Let the straight line x = b divide the area enclosed by y = (1 - x)², y = 0 and x = 0 into two parts R₁(0 ≤ x ≤ b) and R₂ (b ≤ x ≤ 1) such that `R_1 - R_2 = 1/4`. Then b equals `underline(1/2)`.

Explanation: 

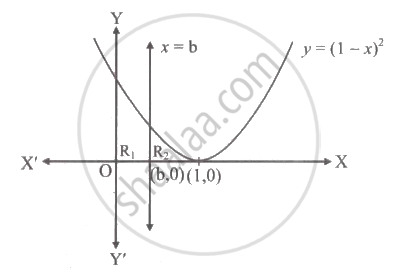
Here, `R_1 = int_0^b (1 - x)^2 dx` and `R_2 = int_b^1 (1 - x)^2 dx`

∴ `R_1 = [(x - 1)^3/3]_0^b` and `R_2 = [(x - 1)^3/3]_b^1`

⇒ `R_1 = (b - 1)^3/3 + 1/3` and `R_2 = -(b - 1)^3/3`

Since `R_1 - R_2 = 1/4`

∴ `(b - 1)^3/3 + 1/3 + (b - 1)^3/3 = 1/4`

⇒ `2/3(b - 1)^3 = -1/12 ⇒ (b - 1)^3 = -1/8`

⇒ b - 1 = `-1/2 ⇒ b = 1/2`