Question

Let the tangent to the parabola S: y² = 2x at the point P(2, 2) meet the x-axis at Q and normal at it meet the parabola S at the point R. Then, the area (in sq.units) of the triangle PQR is equal to ______.

Options

• 25

• `25/2`

• `15/2`

• `35/2`

Answer 1

Let the tangent to the parabola S: y² = 2x at the point P(2, 2) meet the x-axis at Q and normal at it meet the parabola S at the point R. Then, the area (in sq.units) of the triangle PQR is equal to `underlinebb(25/2)`.

Explanation:

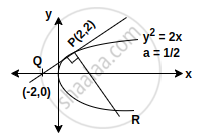
Tangent at P: yy₁ = 2a(x + x₁)

y(2) = `2(1/2)(x + 2)`

⇒ 2y = x + 2

∴ Q = (–2, 0)

Slope of tangent P = `1/2`

Normal at P: y – 2 = `-1/((1/2))(x - 2)`

⇒ y – 2 = –2(x – 2)   ...[∵ m₁m₂ = – 1]

⇒ y = 6 – 2x

∴ Now, solving with y² = 2x ⇒ `"R"(9/2, -3)`

∴ Area(ΔPQR) = `1/2|(2, 2, 1),(-2, 0, 1),(9/2, -3, 1)|`

= `1/2|2(0 + 3) - 2(-2 - 9/2) + 1(+ 6 - 0)|`

= `25/2` sq.units