Question

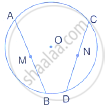
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. prove that:
(i) ∠BMN  = ∠DNM.
(ii) ∠AMN = ∠CNM.

Answer 1

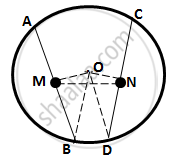
Drop OM⊥AB  and  ON⊥CD

∴ OM bisects AB and ON bisects CD
(Perpendicular drawn from the centre of a circle to a chord bisects it)

⇒ BM =`1/2` AB = `1/2`  CD =DN    .............(1)

Applying Pythagoras theorem,

OM²= OB² -BM²

= OD² - DN²          (by (1))
= ON²

∴ OM=ON

 ⇒  ∠OMN = ⇒ ∠ONM    ……………(2)

(Angles opp to equal sides are equal)

(i) ∠OMB=∠OND         (both 90°)

Subtracting (2) from above,

∠BMN= ∠DNM

(ii) ∠OMA = ONC         (both 90°)
Adding (2) to above,
∠AMN = ∠CNM