Advertisements
Advertisements
Question
Match the following figure:
Advertisements
Solution
(a) The given figure is a cuboid with sides 4, 4 and 6 units.
\[\text { Area of a rectangle } =\text { length }\times \text { width}\]
\[ \therefore \text{Area of the rectangular face sith sides 4 and} 4 =4 \times 4=16\]
\[\text { And, area of the other face with sides 4 and 6 }=4 \times 6=24 \]
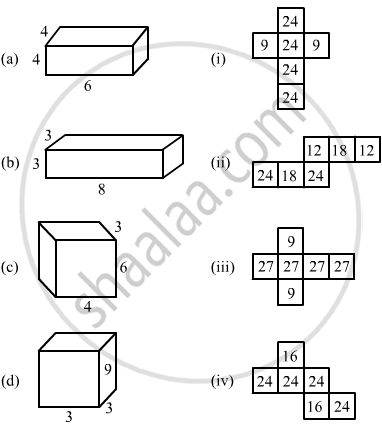
Thus, the net for the given figure will have four faces with area 24 and two faces with area 16.
Observe net (iv) satisfies this.
Thus, the net of figure (a) is net (iv).
(b) The given figure is a cuboid with sides 3, 3 and 8.
\[\text { Area of arectangle }=\text { length }\times \text { width }\]
\[\therefore \text { Area of the rectangular face sith sides 3 and 3 =3 }\times3=9\]
\[\text { And the area of the other face with sides 3 and 8 } =3\times8=24\]
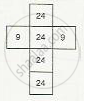
\[\text { Thus, the net for given figure will have four faces with area 24 and two faces with area 9 }.\]
\[\text { Observe that net (i) satisfies this}.\]
\[\text { Thus, the net of figure (b) is net } (i).\]
(c)The given figure is a cuboid with sides 3, 4 and 6.
\[\text { Area of a rectangle }=\text { length }\times \text { width }\]
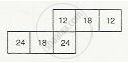
\[ \therefore \text { Area of the rectangular face sith sides 3 and 4 =3 }\times4=12,\]
\[\text { Area of the rectangular face with sides 4 and 6 =4 }\times6=24\]
\[\text { And, area of the other face with sides 3 and 6 =3 }\times6=18\]
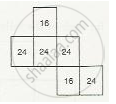
\[\text { Thus, the net for given figure will have two faces with area 24, two faces with area 18 and two faces with area 12. }\]
Observe that net (ii) satisfies this.
Thus, the net of figure (c) is net (ii).
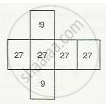
(d) The given figure is a cuboid with sides 3, 3 and 9.
\[\text { Area of arectangle=length }\times \text { width }\]
\[\text { Area of the rectangular face with sides 3 and 3 =3 }\times3=9,\]
\[\text { And, area of the other face with sides 3 and 9 =3 }\times9=27\]
\[\text { Thus, the net for given figure will have four faces with area 27 and two faces with area 9 }.\]
Observe that net (iii) satisfies this.
Thus, the net of figure (d) is net (iii).
RELATED QUESTIONS
The given Figure are prisms or not?
How are pyramids and cones alike?
Here is an incomplete net for making a cube. Complete it in at least two different ways. Remember that a cube has six faces. How many are there in the net here? (Give two separate diagrams. If you like, you may use a squared sheet for easy manipulation.)
Can a polyhedron have for its face 3 triangles?
Name the polyhedron that can be made by folding net:
Using Euler’s formula, find the unknowns.
| Faces | Vertices | Edges |
| 8 | ? | 10 |
How many faces does the following solid have?
Hexahedron
How many vertices does the following solid have?
Sphere
How many vertices does the following solid have?
Octagonal Pyramid
What defines the edges of a solid shape?
