Question

Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______. 

Options

• 47

• 65

• 56

• 12

Answer 1

Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is 65.

Explanation:

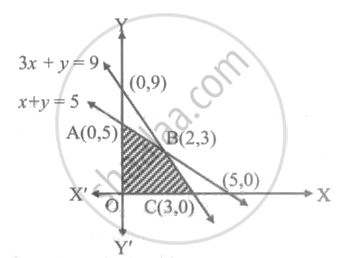
The feasible region lies on origin side of lines
x + y = 5 and 3x + y = 9, in first quadrant.

∴ The comer points of feasible region are 
0 (0, 0), A (0, 5), B (2, 3) and C (3, 0)

∴ Maximum value of objective function
z = 4x + 13y is at A (0, 5)

∴ z = 4(0) + 13(5) = 65