Advertisements
Advertisements
Question
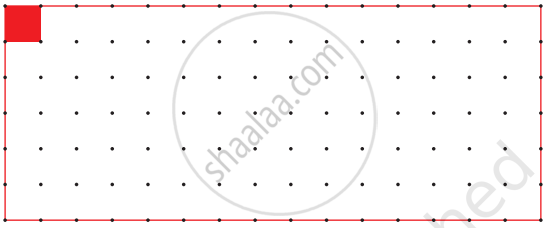
Measure the side of the red square on the dotted sheet. Draw here as many rectangles as possible using 12 such squares.
How many rectangles could you make?
Solution
The side of the square is 1 centimetre.
The following figure shows the possible rectangles using 12 such squares.

There are 7 rectangles.
- 2 rectangles are of size 1 × 12 centimetres.
- 1 rectangle is of size 2 × 6 centimetres.
- 4 rectangles are of size 3 × 4 centimetre
Hence, number of rectangles
= 2 + 1 + 4
= 7
APPEARS IN
RELATED QUESTIONS
The length of a hall is 18 m and its width is 13.5 m. Find the least number of square tiles, each of side 25 cm, required to cover the floor of the hall,
(i) without leaving any margin.
(ii) leaving a margin of width 1.5 m all around. In each case, find the cost of the tiles required at the rate of Rs. 6 per tile
The table given below contains some measures of the square. Find the unknown values.
| Side | Perimeter | Area |
| 6 cm | ? | ? |
A piece of wire is 36 cm long. What will be the length of each side if we form a square
Draw a square B whose side is twice of the square A. Calculate the perimeter of the squares A and B
Each side of a square is 7 m long. Find its perimeter
In the above question, how many square metres of cloth is required to cover all the display boards? What will be the length in m of the cloth used, if its breadth is 120 cm?
The perimeter of a square garden is 48 m. A small flower bed covers 18 sq m area inside this garden. What is the area of the garden that is not covered by the flower bed? What fractional part of the garden is covered by flower bed? Find the ratio of the area covered by the flower bed and the remaining area.
A piece of string is 30 cm long. What will be the length of each side if the string is used to form a square?
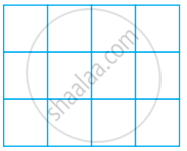
In the given figure, perimeter of (ii) is the same as (i).
 |
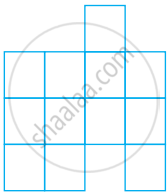 |
| (i) | (ii) |
Three squares are attached to each other as shown in the figure given below. Each square is attached at the mid-point of the side of the square to its right. Find the perimeter of the complete figure.