Question

Minimize z = x + 2y,

Subject to x + 2y ≥ 50, 2x – y ≤ 0, 2x + y ≤ 100, x ≥ 0, y ≥ 0.

Answer 1

First we draw the lines AB, OC and AD whose equations are x + 2y = 50, 2x – y = 0 and 2x + y = 100 respectively.

Line	Equation	Points		Sign	Region
AB	x + 2y = 50	A(50, 0)	B(0, 25)	≥	non-origin side of the line AB
OC	2x – y = 0	O(0, 0)	C(10, 20)	≤	the side where B lies
AD	2x + y = 100	A(50, 0)	D(0, 100)	≤	origin side of the line AD

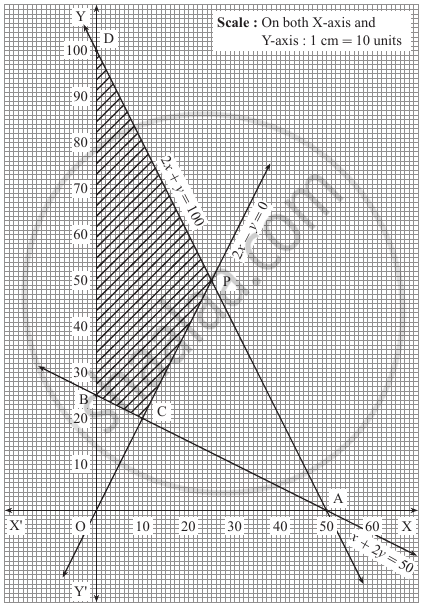
The feasible region is BCPDB which is shaded in the graph.

The vertices of the feasible region are B(0, 25), C(10, 20), P and D(0, 100).

P is the point of intersection of the lines

2x + y = 100     ...(1)

and 2x – y = 0

On adding, we get

4x = 100

∴ x = 25

∴ From (1), 2(25) + y = 100

∴ 50 + y = 100

∴ y = 50

∴ P = (25, 50)

The values of the objective function z = x + 2y at these vertices are

z(B) = 0 + 2(25) = 50,

z(C) = 10 + 2(20) = 50

z(P) = 25 + 2(50) = 125,

z (D) = 0 + 2(100) = 200

∴ z has minimum value 50 at two consecutive vertices B and C.

∴ z has minimum value 50 at every point of segment joining the points B(0, 25) and C(10, 20).

Hence, there are infinite number of optimal solutions.