Advertisements
Advertisements
Question
निम्नलिखित कथन को पढ़िए :
एक समबाहु त्रिभुज तीन रेखाखंडों से बना एक बहुभुज है जिनमें से दो रेखाखंड तीसरे रेखाखंड के बराबर हैं तथा इसका प्रत्येक कोण 60° का है।
इस परिभाषा में, उन पदों को परिभाषित कीजिए जिन्हें आप आवश्यक समझते हैं। क्या इसमें कोई अपरिभाषित पद है? क्या आप इसका औचित्य दे सकते हैं कि एक समबाहु त्रिभुज के सभी कोण और सभी भुजाएँ बराबर होती हैं।
Solution
शब्दों को परिभाषित करने की जरूरत है।
- बहुभुज - एक बंद आकृति जो तीन या अधिक रेखाखंडों से घिरी हो।
- रेखाखंड - रेखा का वह भाग होता है जिसके दो सिरे होते हैं।
- रेखा - अपरिभाषित पद।
- बिंदु - अपरिभाषित पद।
- कोण - एक उभयनिष्ठ प्रारंभिक बिंदु वाली दो किरणों से बनी आकृति।
- न्यून कोण - वह कोण जिसकी माप 0° से 90° के बीच होती है।
यहाँ अपरिभाषित पद रेखा और बिंदु हैं।
एक समबाहु त्रिभुज के सभी कोण 60° के होते हैं। ...(दिया गया है।)
दो रेखाखंड तीसरे के बराबर हैं। ...(दिया गया है।)
इसलिए, एक समबाहु त्रिभुज की तीनों भुजाएँ बराबर होती हैं, क्योंकि यूक्लिड के अभिगृहीत के अनुसार, जो चीज़ें एक ही चीज़ के बराबर होती हैं, वे एक-दूसरे के बराबर होती हैं।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
लम्ब रेखाएँ
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
रेखाखंड
यूक्लिड की अभिगृहीतों की सूची में दिया हुआ अभिगृहीत 5 एक सर्वव्यापी सत्य क्यों माना
जाता है? (ध्यान दीजिए कि यह प्रश्न पाँचवीं अभिधरणा से संबंधित नहीं है।)
थेल्स निम्नलिखित देश का वासी था :
पाइथागोरस एक विद्यार्थी था :
‘रेखाएँ समांतर होती हैं, यदि वे प्रतिच्छेद नहीं करती’ का कथन, निम्नलिखित के रूप में दिया गया है :
यदि एक राशि B एक अन्य राशि A का एक भाग है, तो A को B और एक अन्य राशि C के योग के रूप में लिखा जा सकता है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
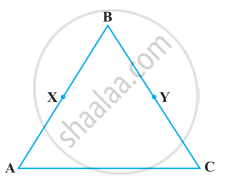
निम्नलिखित आकृति में, हमें प्राप्त है :
BX = `1/2` AB, BY = `1/2` BC तथा AB = BC है। दर्शाइए कि BX = BY है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
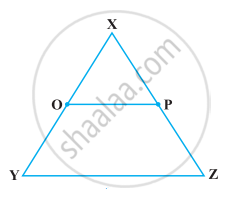
निम्नलिखित आकृति में, यदि OX = `1/2` XY, PX = `1/2` XZ और OX = PX हो, तो दर्शाइए कि XY = XZ है।
निम्नलिखित कथन का अध्ययन कीजिए :
“दो प्रतिच्छेदी रेखाएँ एक ही रेखा पर लंब नहीं हो सकती हैं।”
जाँच कीजिए कि क्या यह कथन यूक्लिड पाँचवीं अभिधारणा का समतुल्य रूपांतरण है।
[संकेत : उपरोक्त कथन में, दो प्रतिच्छेदी रेखा l और m तथा एक अन्य रेखा n की पहचान कीजिए।]
