Question

O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.

Answer 1

 

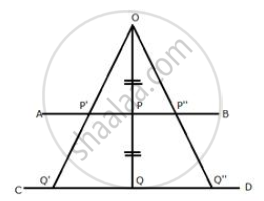
P moves along AB, and Q moves in such a way that PQ is always equal to OP.
But P is the mid-point of OQ
Now in ΔOQQ’
P' and P'' are the mid-points of OQ' and OQ''
Therefore, AB ∥ Q'Q''
Therefore, Locus of Q is a line CD which is parallel to AB.