Question

Observe the figures given below carefully and answer the questions:

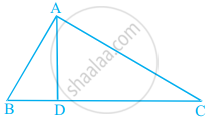
Figure A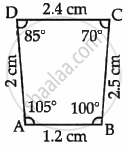
Figure B
Figure C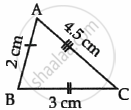

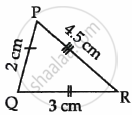1. Name the figure(s) where in two figures are similar.
2. Name the figure(s) where in the figures are congruent.
3. 1. Prove that congruent triangles are also similar but not the converse.
      OR
   2. What more is least needed for two similar triangles to be congruent?

Answer 1

1. Figures A and C are similar.
2. Only Figure C is congruent.
3. 1. All congruent figures are similar but all similar figures are not congruent.
      For example, a pair of triangles that are similar by the A.A.A. test of similarity are not congruent pairs of triangles since the exact lengths of the sides are unknown.
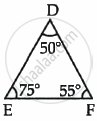
      In ΔABC and ΔDEF,
      ∠A = ∠D = 50°,
      ∠B = ∠E = 75°
      and ∠C = ∠F = 55°.
      Hence, ΔABC ∼ ΔDEF but they are not congruent.
      OR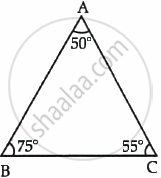
   2. The length of corresponding sides must be equal.