Question

Obtain an expression for the energy stored in a charged condenser. Express it in different forms. 

Answer 1

1. Consider a capacitor of capacitance C being charged by a DC source of V volts as shown in the figure below.
   
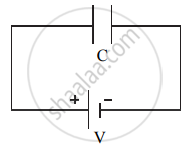
   A capacitor charged by a DC source
2. During the process of charging, let q' be the charge on the capacitor and V be the potential difference between the plates. Hence C = `"q"/"V"`
3. A small amount of work is done if a small charge dq is further transferred between the plates.
   ∴ dW =  V dq = `("q"^')/"C"`dq
4. Total work done in transferring the charge
   W = `int"dW" = int_0^"Q" "q"^'/"C" "dq" = 1/"C" int_0^"Q" "q"^'` dq
   = `1/"C"[("q"^')^2/2]_0^"Q" = 1/2 "Q"^2/"C"`
5. This work done is stored as electrical potential energy U of the capacitor. This work done can be expressed in different forms as follows.
   ∴ U = `1/2 "Q"^2/"C" = 1/2 "CV"^2 = 1/2 "QV"`  ….(∵ Q = CV)