Question

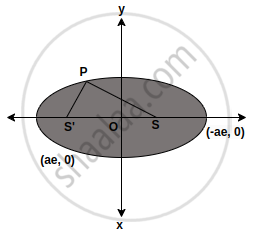
On the ellipse `x^2/8 + "y"^2/4` = 1 let P be a point in the second quadrant such that the tangent at P to the ellipse is perpendicular to the line x + 2y = 0. Let S and S' be the foci of the ellipse and e be its eccentricity. If A is the area of the triangle SPS' then, the value of (5 – e²). A is ______.

Options

• 24

• 6

• 14

• 12

Answer 1

On the ellipse `x^2/8 + "y"^2/4` = 1 let P be a point in the second quadrant such that the tangent at P to the ellipse is perpendicular to the line x + 2y = 0. Let S and S' be the foci of the ellipse and e be its eccentricity. If A is the area of the triangle SPS' then, the value of (5 – e²) A is 6.

Explanation:

Let `"P"(sqrt(8)cosθ, 2sinθ)` lies at `x^2/8 + "y"^2/4` = 1,

Equation of tangent at point P,

`x/sqrt(8)cosθ + "y"/2sinθ - 1` = 0

Slope = `(-1)/sqrt(2)cotθ` = 2, because it is perpendicular to x + 2y = 0 whose slope is `(-1)/2`

⇒ cotθ = `-2sqrt(2)`

⇒ cosθ = `(-2sqrt(2))/3`, sinθ = `1/3`,

So, point `"P"((-8)/3, 2/3)`

∴ Area(A) = `1/2 xx 4 xx 2/3 = 4/3`

e² = `1 - 4/8`

⇒ e = `1/sqrt(2)`

So, (5 – e²)A = `(5 - 1/2) xx 4/3` = 6