Question

P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.

Answer 1

We have,

AB = AP + PB = (3 + 6) cm = 9 cm and, AC = AQ + QC = (5 + 10) cm = 15 cm.

`\therefore \frac{AP}{AB}=\frac{3}{9}=\frac{1}{3}\text{ and }\frac{AQ}{AC}=\frac{5}{15}=\frac{1}{3}`

`\Rightarrow \frac{AP}{AB}=\frac{AQ}{AC}`

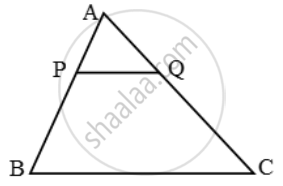
Thus, in triangles APQ and ABC, we have

`\frac{AP}{AB}=\frac{AQ}{AC} and ∠A = ∠A `

Therefore, by SAS-criterion of similarity, we have

∆APQ ~ ∆ABC

`\Rightarrow \frac{AP}{AB}=\frac{PQ}{BC}=\frac{AQ}{AC}`

`\Rightarrow \frac{PQ}{BC}=\frac{AQ}{AC}\Rightarrow\frac{PQ}{BC}=\frac{5}{15}`

`\Rightarrow \frac{PQ}{BC}=\frac{1}{3}`

⇒ BC = 3PQ