Advertisements
Advertisements
Question
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
Options
mg
\[\text{ mg} - \frac{\text{mv}^2}{\text{R}}\]
\[\text{mg} + \frac{\text{mv}^2}{\text{R}}\]
zero.
Solution
zero
When the car is in air, the acceleration of bob and car is same. Hence, the tension in the string will be zero.
APPEARS IN
RELATED QUESTIONS
A stone of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40 rev/min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A smooth block loosely fits in a circular tube placed on a horizontal surface. The block moves in a uniform circular motion along the tube. Which wall (inner or outer) will exert a nonzero normal contact force on the block?
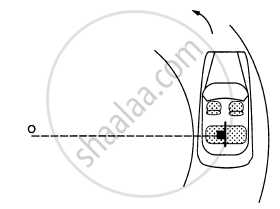
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.

A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
A train A runs from east to west and another train B of the same mass runs from west to east at the same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
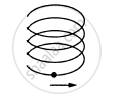
A particle is going in a spiral path as shown in figure with constant speed.
A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0 t where v is cm/s and t in seconds.
(a) Find the radial acceleration of the particle at t = 1 s.
(b) Find the tangential acceleration at t = 1 s.
(c) Find the magnitude of the acceleration at t = 1 s.
Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (In the following figure). A small block of mass 100 g is kept on the seat which rests against the plate. the friction coefficient between the block and the plate is. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
In non-uniform circular motion, the ratio of tangential to radial acceleration is (r = radius, a = angular acceleration and v = linear velocity)
A wheel is subjected to uniform angular acceleration about its axis. The wheel is starting from rest and it rotates through an angle θ1, in first two seconds. In the next two seconds, it rotates through an angle θ2. The ratio θ1/θ2 is ____________.
A rope is wound around a solid cylinder of mass 1 kg and radius 0.4 m. What is the angular acceleration of cylinder, if the rope is pulled with a force of 25 N? (Cylinder is rotating about its own axis.)
The real force 'F' acting on a particle of mass ' m' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of the magnitude of such force is (T = periodic time).
Angular displacement (θ) of a flywheel varies with time as θ = at + bt2 + ct3 then angular acceleration is given by ____________.
In negotiating curve on a flat road, a cyclist leans inwards by an angle e with the vertical in order to ______.
A body is moving along a circular track of radius 100 m with velocity 20 m/s. Its tangential acceleration is 3 m/s2 then its resultant accelaration will be ______.
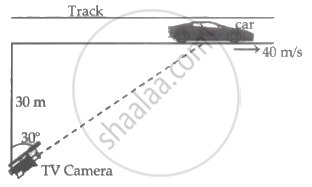
A racing car is travelling along a track at a constant speed of 40 m/s. A T.V. cameraman is recording the event from a distance of 30 m directly away from the track as shown in the figure. In order to keep the car under view in the position shown, the angular speed with which the camera should be rotated is ______.
Statement I: A cyclist is moving on an unbanked road with a speed of 7 kmh-1 and takes a sharp circular turn along a path of radius of 2 m without reducing the speed. The static friction coefficient is 0.2. The cyclist will not slip and pass the curve. (g = 9.8 m/s2)
Statement II: If the road is banked at an angle of 45°, cyclist can cross the curve of 2 m radius with the speed of 18.5 kmh-1 without slipping.
In the light of the above statements, choose the correct answer from the options given below.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed?
