Advertisements
Advertisements
Question
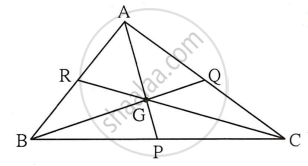
Point G is the centroid of Δ ABC.
If l(AP) = 6 then l(AG) = ______ and l(GP) = ______.
Fill in the Blanks
Solution
If l(AP) = 6 then l(AG) = 4 and l(GP) = 2.
Explanation:
In ∆ABC, the medians AP, BQ and CR to the sides BC, CA and AB respectively intersect at G. Since, centroid of a triangle divides the medians in the ratio of 2 : 1, then AG : GP = BG : GQ = CG : GR = 2 : 1.
We have, AG : GP = 2 : 1
⇒ `("AG")/("GP") = 2/1`
⇒ `("AG")/("AP" - "AG") = 2`
⇒ `("AG")/(6 - "AG")` = 2
⇒ 2(6 − AG) = AG
⇒ 12 − 2AG = AG
⇒ 3AG = 12
⇒ `"AG" = 12/3`
⇒ AG = 4
shaalaa.com
Is there an error in this question or solution?
